在长方形ABCD的世界里，点E落在AD边上，将AD分成了3厘米和6厘米的两段。当∠BEC恰好为60°时，△BCE的面积就成了一个充满悬念的谜题。 想象一下，长方形的边长相交，在E点处勾勒出的60°角，仿佛是一把钥匙，能打开△BCE面积的秘密之门。那几条线段的长度，看似简单的数字，却在几何的魔法下，与角度交织出独特的面积答案。 你是否能从这长方形的布局、线段的长短以及特殊的角度中，窥探出△BCE面积的真容呢？它就像藏在几何迷宫里的宝藏，等待着你用智慧去发掘。
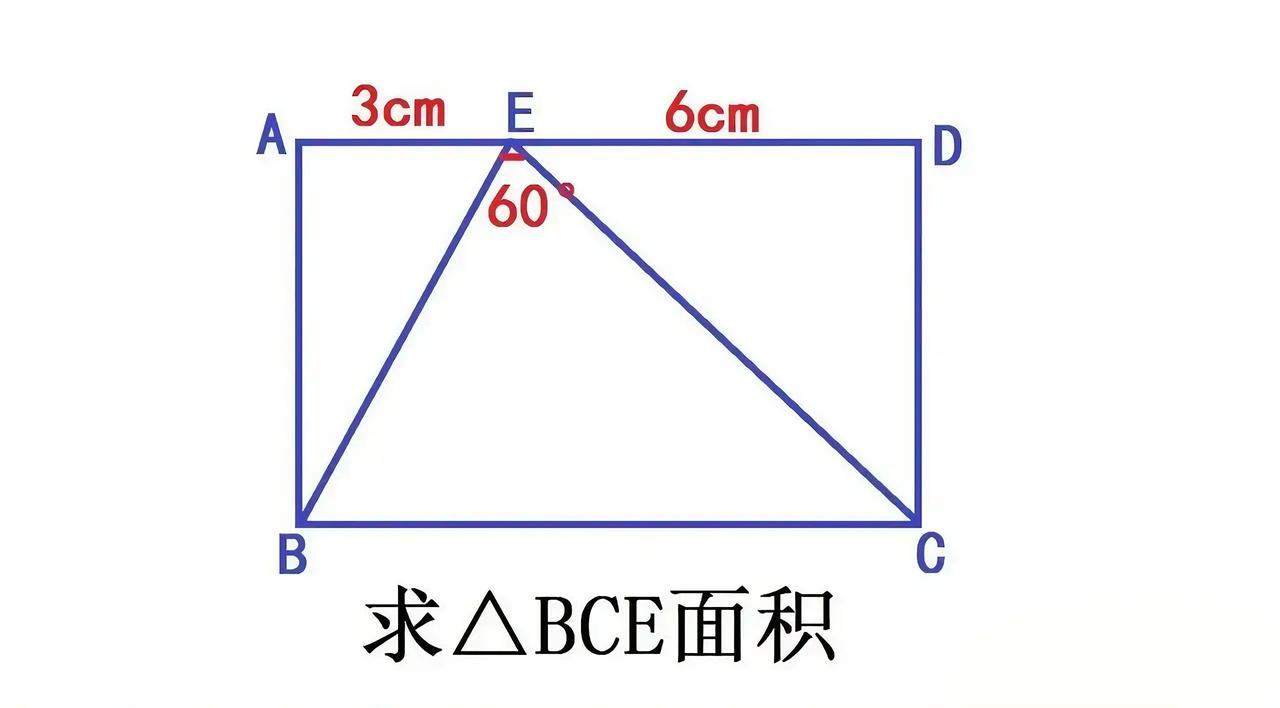
在长方形ABCD的世界里，点E落在AD边上，将AD分成了3厘米和6厘米的两段。当
大力小学数学吖
2025-10-23 22:54:36
0
阅读：33
![卢伟冰有一点真的很强：和谁在一起都很搭，风格和融洽。[doge][doge][doge]](http://image.uczzd.cn/10806253299371667567.jpg?id=0)
![谁都不服，就服现在的年轻人[6]](http://image.uczzd.cn/11320752667833125987.jpg?id=0)
![最新卫星图显示仅仅短短三天间隔，004就多了一截[666]这搭载速度好快！图源](http://image.uczzd.cn/13456552088981606623.jpg?id=0)
用户81xxx78
初中就只能做三角形的外接圆。找到120度角，再求半径。
武寒旭
设AB为ⅹ，可求BE和CE。三角形BEC为60度，列关于BC方程可求解。太简单就不计算了。