[LG]《Bridging Kolmogorov Complexity and Deep Learning: Asymptotically Optimal Description Length Objectives for Transformers》P Shaw, J Cohan, J Eisenstein, K Toutanova [Google DeepMind & Google Research] (2025)
深度学习与Kolmogorov复杂度的桥梁:为Transformer设计渐近最优描述长度目标
• MDL原则将机器学习视为数据压缩,寻找模型与数据整体描述长度最短者,理论上能提升泛化能力。
• Transformer虽计算强大,但缺乏统一的模型复杂度度量,阻碍MDL原则的直接应用。
• 本文基于Kolmogorov复杂度和Transformer的计算普适性,证明存在渐近最优的描述长度目标,保证随着模型资源无限增加,压缩近乎最优。
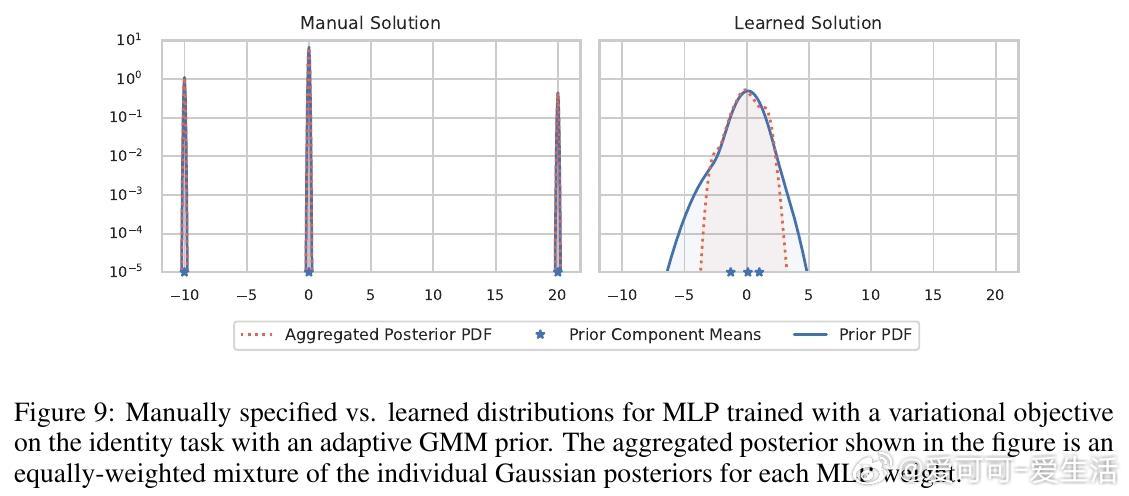
• 构造了基于自适应高斯混合模型(GMM)先验的可微分变分目标,兼顾理论最优与实际可训练性。
• 实验以计算奇偶性任务为例,展示该目标能挑选低复杂度且泛化强的模型,但标准优化器难以从随机初始化找到最优解,揭示优化挑战。
• 理论框架为未来设计具备强压缩和泛化能力的神经网络训练目标指明方向。
心得:
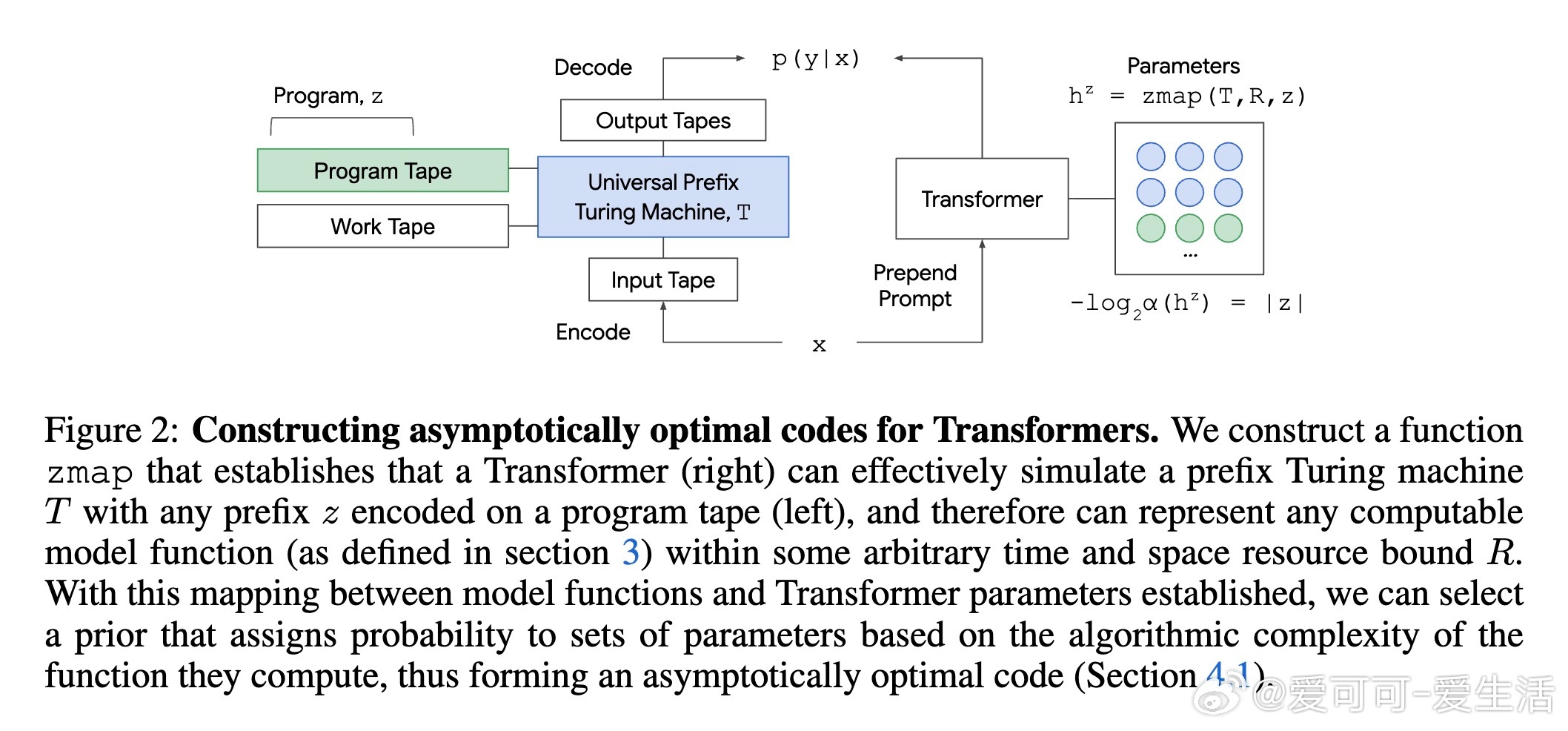
1. 计算普适性让Transformer可模拟任意图灵机,理论上具备表达任何可计算函数的能力,这是实现渐近最优编码的核心保证。
2. 传统随机初始化难以找到低复杂度解,表明优化路径设计和先验建模同等重要,未来需探索更适合复杂变分目标的训练策略。
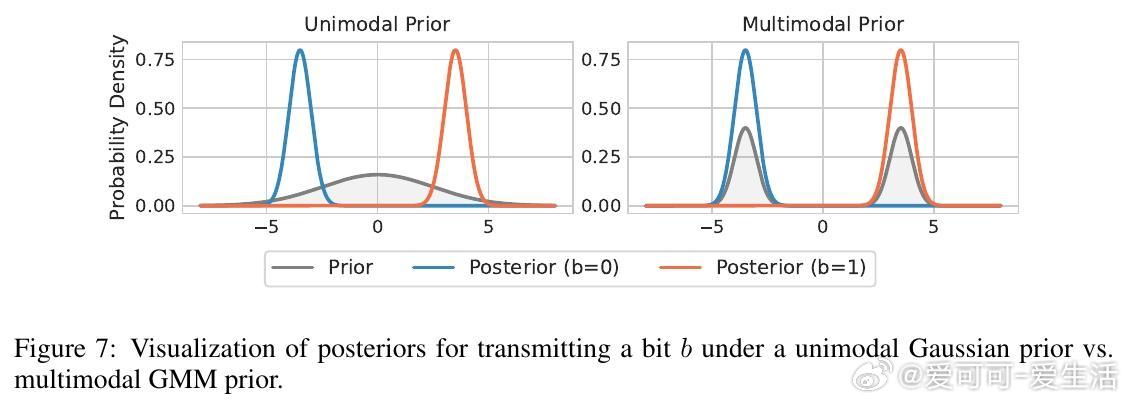
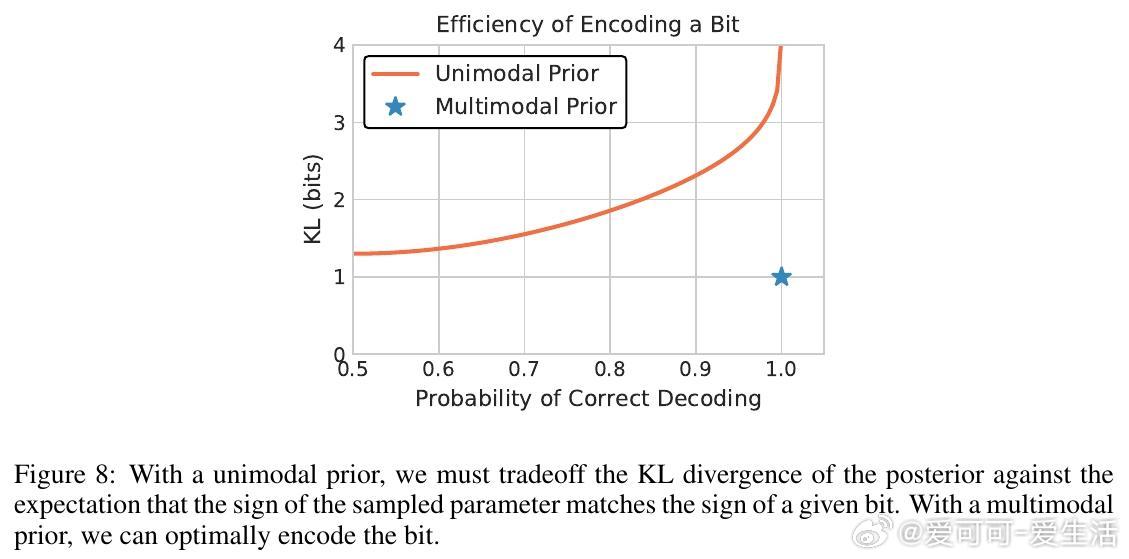
3. 变分编码引入的多模态GMM先验有效提升编码效率,体现了“软量化”与复杂度压缩的深层联系,对网络压缩和高效微调有实用价值。
详情🔗arxiv.org/abs/2509.22445
机器学习 深度学习 Kolmogorov复杂度 MDL原则 Transformer 模型压缩 理论AI