如何证明 √2 + √3 + √5 + √7 是无理数? 这里有一个绝妙证法: 令b=√2+√3+√5+√7, 注意到有 √7=151*b^15 / 32473600 +1312971*b13/2078310400 +6241559*b^11/207831040 +1364453637*b^9 /2078310400 +3626646037*b^7/519577600 +71310531461*b^5/2078310400 +67424441651*b^3 / 1039155200 +12200206607*b/415662080, 因此,若b为有理数,则有理数的加减乘除仍然是有理数,那么根据上式,√7也是有理数,这不可能,因此原假设不成立,b是无理数。



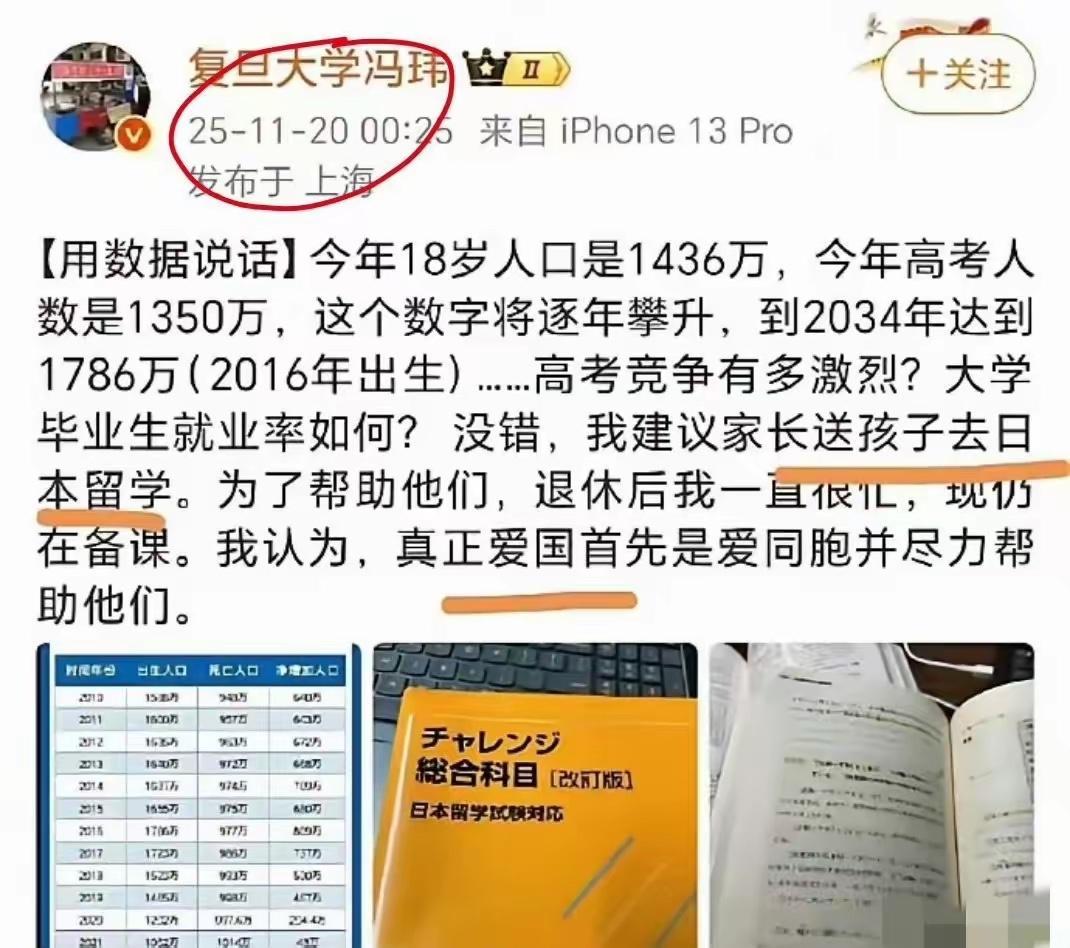



![复旦大学冯玮微博发文:建议家长送孩子去日本留学!!!!!!!!……[大笑][](http://image.uczzd.cn/2052974597624623381.jpg?id=0)

